
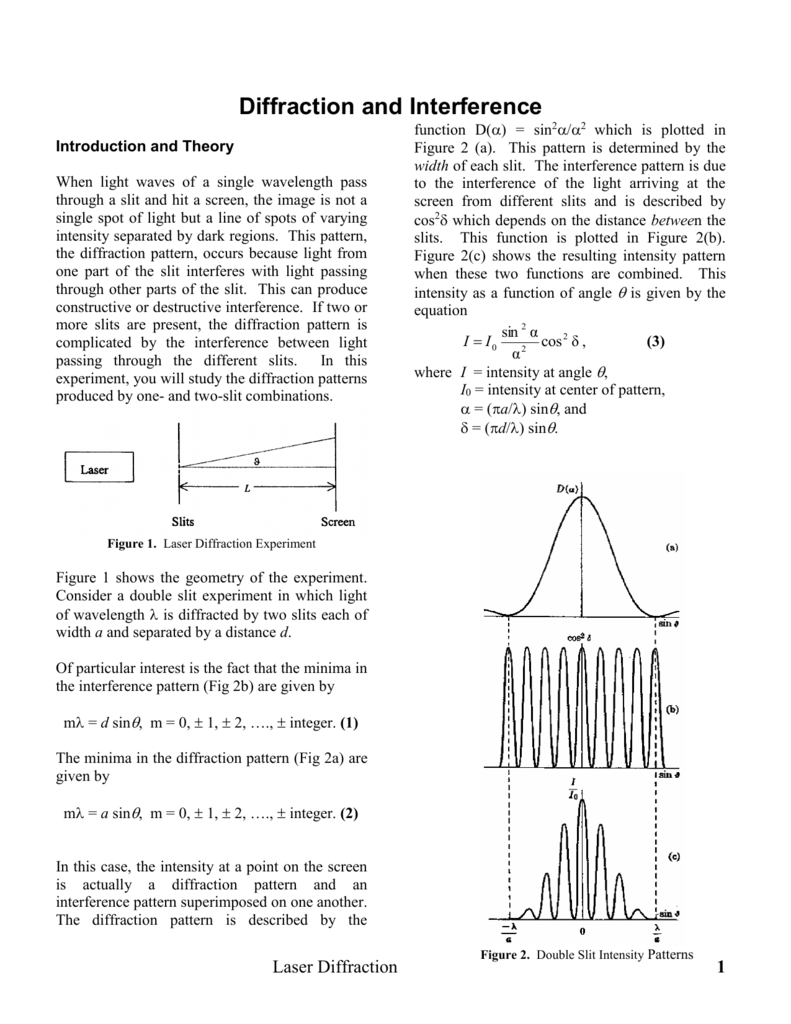
The laser pointer was put at an almost normal angle (90°) to the microdisc array, as illustrated in Fig. As an extra task, the students can use the same experimental approach to quantify the pixel pitch in their mobile phone screens. Their task is to use laser diffraction to determine the pattern on the samples. For the experiment, the students are given a set of labelled samples with unknown patterns, as well as a laser pointer with a holder, a paper screen and a tape measure. In the diffraction measurements the largest features are observed as the smallest diffraction features, and vice versa, which is an example of the general rule that small features in real space become large in reciprocal space. The samples have features on three different length scales, ranging from the microdisc size, w, via the lattice spacings, a, to the overall size of the array, s. However, we found that the diffracted intensity was much stronger in reflection geometry. Initially, we fabricated the arrays on transparent Si 3N 4 membranes, which made it possible to perform the experiment in transmission (Laue) geometry. The overall size of the pattern is about 0.5–1 mm, in order to fit within the laser spot. Manufacturing structures of this size is straightforward with EBL, but also well within the reach of lower-resolution patterning techniques.

1 ▸( c) is a high-magnification SEM image of the edge of a microdisc at a 30° tilt, showing a thickness of about 200 nm. This particular sample has circular microdiscs with a diameter of w = 3 µm and lattice spacings of a 1 = 5 µm and a 2 = 10 µm in the horizontal and vertical directions, respectively. ( d) Schematic of the diffraction geometry.Ī scanning electron microscopy (SEM) image of a typical sample is shown in Fig. ( c) Higher-magnification SEM image, tilt 30°, showing the edge of a single microdisc (scale bar 300 nm). ( b) Microscopy image of an Au microdisc array (scale bar 10 µm).

( a) Experimental setup to demonstrate the reciprocal space with laser diffraction from an Au microdisc array. The laser diffraction experiment is complemented by an X-ray diffraction experiment using metal powders. The experiment presented here is part of an undergraduate course in X-ray physics, based on the textbook by Als-Nielsen & McMorrow (2011 ▸). The required feature sizes are fully compatible with lower-resolution methods such as UV lithography. This is a standard method in semiconductor fabrication, and its great flexibility makes it easy to fabricate samples that illustrate various concepts. We used artificial arrays of Au microdiscs on silicon wafers, created with electron beam lithography (EBL). Optical experiments of diffraction for educational purposes have previously been reported using gratings (Burch et al., 1985 ▸ Logiurato et al., 2020 ▸), overhead projector films (Ferralis et al., 2004 ▸), microdisplays (Lehmann et al., 2019 ▸) and nanowire arrays (Hannibal Madsen et al., 2013 ▸). To carry out an experiment with Bragg diffraction using visible light, the crystal lattice spacing should be in the micrometre range. Here, we demonstrate how laser diffraction can be used for student experiments in diffraction and reciprocal space. However, the wavelengths of lasers are generally too large for atomic diffraction. The most readily available source of coherent radiation is laser beams, which can be generated by low-cost battery-driven laser pointers. X-rays require radiation protection, whereas electron beams require a vacuum. Crystallography of atomic crystals is normally performed with X-rays, electrons or neutrons, which is experimentally challenging in an undergraduate teaching context. Laboratory experiments can be a powerful tool to support student learning, but they are difficult to realize in the case of diffraction. The concepts of diffraction and reciprocal space are quite challenging for undergraduate students (Radford, 1975 ▸). Any in-depth description of diffraction, beyond Bragg’s law, requires the introduction of reciprocal space, which is also used in many other areas of physics. Crystal diffraction is a vital tool in many fields of science, in particular solid state physics.


 0 kommentar(er)
0 kommentar(er)
